Било је доба када је телефонирало на удаљеним местима, требало је ставити уста врло близу предајника, говорити врло полако и врло гласно, тако да особа са другог краја може јасно чути поруку. Данас чак можемо да упућујемо видео позиве широм света са висококвалитетним резолуцијама. Тајна тако страховитог развоја технологије лежи у томе Електрична филтер теорија и Теорија далековода . Електрични филтри су кола која пролазе само одабрани опсег фреквенција, док пригушују друге нежељене фреквенције. Један од таквих филтера је Високопропусни филтер .
Шта је високопропусни филтер?
Дефиниција високопропусног филтера је филтер који пропушта само оне сигнале чије су фреквенције веће од граничних фреквенција, чиме умањују сигнале нижих фреквенција. Вредност граничне фреквенције зависи од дизајна филтера.
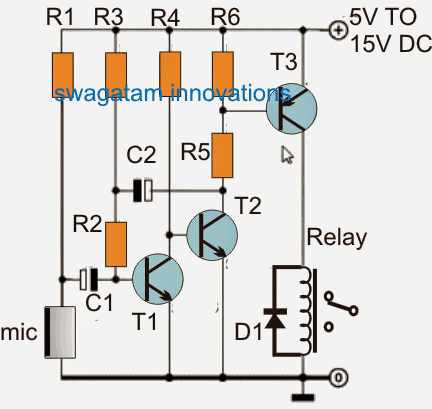
Круг високопропусног филтера
Основни високопропусни филтер изграђен је серијским повезивањем кондензатор и отпорник . Док се улазни сигнал примењује на кондензатор , излаз се повлачи преко отпорник .

Круг високопропусног филтера
У овом распореду кола, кондензатор има високу реактанцу на нижим фреквенцијама, па делује као отворени круг на нискофреквентне улазне сигнале све док се не постигне гранична фреквенција „фц“. Филтер пригушује све сигнале испод нивоа граничне фреквенције. На фреквенцијама изнад одсеченог нивоа фреквенције реактанција кондензатора постаје мала и делује као кратки спој на те фреквенције, омогућавајући им тако да прођу директно на излаз.
Пасивни РЦ високопропусни филтер
Изнад приказани високопропусни филтер познат је и као Пасивни РЦ високопропусни филтер пошто је коло изграђено само користећи пасивни елементи . За рад филтера није потребно примењивати спољно напајање. Овде је кондензатор реактивни елемент и излаз се повлачи преко отпорника.
Карактеристике високопропусног филтра
Кад говоримо о гранична фреквенција позивамо се на тачку у фреквенцијски одзив филтра при чему је појачање једнако 50% вршног појачања сигнала, тј. 3дБ вршног добитка. У високопропусном филтру појачање се повећава са повећањем фреквенција.

Крива фреквенције високопропусног филтра
Ова гранична фреквенција фц зависи од вредности Р и Ц кола. Овде је Временска константа τ = РЦ, гранична фреквенција је обрнуто пропорционална временској константи.
Пресечна фреквенција = 1 / 2πРЦ
Коначни добитак се даје са АВ = Воут / Вин
тј. АВ = (Воут) / (В ин) = Р / √ (Рдва+ Ксцдва) = Р / З
На ниској фреквенцији ф: Ксц → ∞, Воут = 0
На високофреквентном ф: Ксц → 0, Воут = Вин
Фреквенцијски одзив високопропусног филтра или дијаграм боде филтра високог пролаза
У високопропусном филтру све фреквенције које леже испод граничне фреквенције „фц“ су пригушене. На овој тачки пресека фреквенције добијамо појачање од -3дБ и у овом тренутку ће реактанса вредности кондензатора и отпорника бити једнака, тј. Р = Ксц. Добитак се израчунава као
Добитак (дБ) = 20 лог (Воут / Вин)
Нагиб криве високопропусног филтра је +20 д Б / деценију, тј. након проласка нивоа граничне фреквенције, излазни одзив кола се повећава са 0 на Вин брзином од +20 дБ по деценији, што је повећање од 6 дБ по октави.

Фреквентни одзив високопропусног филтра
Област од почетне тачке до тачке пресека фреквенције позната је као зауставни опсег јер ниједна фреквенција не сме проћи. Подручје изнад тачке граничне фреквенције. односно -3 дБ тачка је позната као пассбанд . На граничној фреквенцији, амплитуда тачкастог излазног напона износиће 70,7% улазног напона.
Ево пропусност филтра означава вредност фреквенције са које смеју да пролазе сигнали. На пример, ако је ширина опсега високопропусног филтра дата као 50 кХз, то значи да је дозвољено да пролазе само фреквенције од 50 кХз до бесконачности.
Фазни угао излазног сигнала је +450 на граничној фреквенцији. Формула за израчунавање фазног помака високопропусног филтра је
∅ = арктан (1 / 2πфРЦ)

Крива фазног померања
У практичној примени, излазни одзив филтра се не протеже до бесконачности. Електрична карактеристика филтарских елемената примењује ограничење на одзив филтра. Правилним одабиром компонената филтра можемо прилагодити опсег фреквенција које се пригушују, опсег који треба пренијети итд ...
Високопропусни филтер помоћу оптичког појачала
У овај високопропусни филтер заједно са пасивним елементима филтера додајемо Оп-амп до кола. Уместо да добијемо бесконачни излазни одговор, овде је излазни одговор ограничен отвореном петљом карактеристике Оп-појачала . Отуда овај филтер делује као а пропусни филтер са граничном фреквенцијом која је дефинисана ширином опсега и карактеристикама појачања Оп-појачала.

Високопропусни филтер помоћу оптичког појачала
Појачање напона отворене петље Оп-појачала делује као ограничење ширине опсега појачало . Појачање појачала смањује се на 0 дБ са повећањем улазне фреквенције. Одзив кола је сличан пасивном високопропусном филтру, али овде појачање Оп-појачавача појачава амплитуду излазног сигнала.
Тхе добитак филтера коришћење неинвертујућег Оп-појачала дато је са:
АВ = Воут / Вин = (Искључено (ф / фц)) / √ (1+ (ф / фц) ^ 2)
где је Аф добитак опсега филтра = 1+ (Р2) / Р1
ф је фреквенција улазног сигнала у Хз
фц је гранична фреквенција
Када ниска толеранција отпорници и кондензатори који се користе, ови високопропусни активни филтери пружају добру тачност и перформансе.
Активни високопропусни филтер
Високопропусни филтер помоћу оптичког појачала је такође познат као ан активни високопропусни филтер јер заједно са пасивним елементима кондензатор и отпорник активни елемент Оптичко појачало се користи у колу . Коришћењем овог активног елемента можемо контролисати граничну фреквенцију и опсег излазног одзива филтра.
Високопропусни филтер другог реда
Сви кругови филтера које смо до сада видели сматрају се високопропусним филтерима првог реда. У високопропусном филтру другог реда, додатни блок РЦ мреже додаје се у високопропусни филтер првог реда на улазној путањи.
Високопропусни филтер другог реда
Тхе фреквенцијски одзив високопропусног филтера другог реда је сличан високопропусном филтеру првог реда. Али у опсегу заустављања високопропусног филтра другог реда биће двоструко већи од филтра првог реда при 40дБ / Децаде. Филтери вишег реда могу се формирати каскадним филтрима првог и другог реда. Иако нема ограничења за редослед, величина филтера се повећава заједно са њиховим редоследом и тачност се погоршава. Ако је у филтеру вишег реда Р1 = Р2 = Р3 итд ... и Ц1 = Ц2 = Ц3 = итд ..., тада ће гранична фреквенција бити иста без обзира на редослед филтера.

Високопропусни филтер другог реда
Гранична фреквенција високопропусног активног филтера другог реда може се дати као
фц = 1 / (2π√ (Р3 Р4 Ц1 Ц2))
Функција преноса високопропусног филтера
Како се импеданса кондензатора често мења, електронски филтри имају одзив зависан од фреквенције.
Комплексна импеданса кондензатора дата је као Зц = 1 / сЦ
Где је с = σ + јω, ω угаона фреквенција у радијанима у секунди
Преносна функција кола може се наћи помоћу стандардних техника анализе кола као што су Охмов закон , Кирцххофф-ови закони , Суперпозиција итд. Основни облик преносне функције дат је једначином
Х (с) = (ам с ^ м + а (м-1) с ^ (м-1) + ⋯ + а0) / (бн с ^ н + б (н-1) с ^ (н-1) + ⋯ + б0)
Тхе редослед филтера је познат по степену називника. Пољаци и нуле кола се издвајају решавањем корена једначине. Функција може имати стварне или сложене корене. Начин на који се ови корени наносе на с равни, где је σ означено хоризонталном осом, а ω вертикалном осом, открива пуно информација о колу. За високопропусни филтер, нула се налази у исходишту.
Х (јω) = Воут / Вин = (-З2 (јω)) / (З1 (јω))
= - Р2 / (Р1 + 1 / јωЦ)
= -Р2 / Р1 (1 / (1+ 1 / (јωР1 Ц))
Ево Х (∞) = Р2 / Р1, појачати када ω → ∞
τ = Р1 Ц и ωц = 1 / (τ), тј. ωц = 1 / (Р1Ц) је гранична фреквенција
Тако је преносна функција високопропусног филтра дата са Х (јω) = - Х (∞) (1 / (1+ 1 / јωτ))
= - Х (∞) (1 / (1- (јωц) / ω))
Када је улазна фреквенција мала онда је З1 (јω) велика, па је излазни одзив низак.
Х (јω) = (- Х (∞)) / √ (1+ (ωц / ω) ^ 2) = 0 када је ω = 0 Х (∞) / √2 када ω = ω_ц
и Х (∞) када је ω = ∞. Овде негативни знак указује на фазни помак.
Када је Р1 = Р2, с = јω и Х (0) = 1
Дакле, преносна функција високопропусног филтра Х (јω) = јω / (јω + ω_ц)
Маслац вредан високопропусног филтера
Поред одбацивања нежељених фреквенција, идеалан филтер такође треба да има уједначену осетљивост за жељене фреквенције. Такав идеалан филтер је непрактичан. Али Степхен Буттер вредан у свом раду „О теорији појачивача филтера“ показао је да се овакав тип филтера може постићи повећањем броја филтарских елемената праве величине.
Маслац вредан филтера је дизајниран на такав начин да даје равни фреквенцијски одзив у пропусном опсегу филтра и смањује се према нули у зауставном опсегу. Основни прототип Маслац вредан филтера је нископропусни дизајн али модификацијама високог пролаза и опсежни филтери може се дизајнирати.
Као што смо видели горе, за јединицу филтра високог пролаза првог реда добитак је Х (јω) = јω / (јω + ω_ц)
За н таквих филтера у серији Х (јω) = (јω / (јω + ω_ц)) ^ н која је по решавању једнака

„Н“ контролише редослед преласка између опсега проласка и зауставног опсега. Према томе, бржи прелаз убрзајте, тако да при н = ∞ филтер вредан маслаца постаје идеалан високопропусни филтер.
Током примене овог филтера ради једноставности узимамо у обзир ωц = 1 и решавамо функцију преноса
за с = јω. тј. Х (с) = с / (с + ωц) = с / (с + 1) за поруџбину 1:
Х (с) = с ^ 2 / (с ^ 2 + ∆ωс + (ωц ^ 2) за поруџбину 2
Стога је преносна функција каскаде у високопропусном филтру


Парцела маслаца Боде вредна високопропусног филтера
Примене високопропусних филтера
Примјене високопропусних филтера углавном укључују следеће.
- Ови филтери се користе у звучницима за појачање.
- Високопропусни филтер се користи за уклањање нежељених звукова близу доњег краја звучног опсега.
- Да би се спречило појачавање Једносмерна струја који би могли да оштете појачало, за проводнике наизменичне струје користе се високопропусни филтри.
- Високопропусни филтер Обрађиванње слике : Високопропусни филтери се користе у обради слике за изоштравање детаља. Применом ових филтера преко слике можемо преувеличати сваки ситни део детаља на слици. Али претјеривање може оштетити слику јер ови филтери појачавају шум на слици.
У дизајну ових филтера мора се још много тога постићи како би се постигли стабилни и идеални резултати. Ови једноставни уређаји играју значајну улогу у разним контролни системи , аутоматски системи, обрада слике и звука. Који од примена Високопропусни филтер јеси ли наишао?